해당 자료는 전북대학교 이영미 교수님 2023고급시계열분석 자료임

패키지 설치

############## package
library(forecast) #ma
library(TTR) #sma
library(lmtest) #dwtest

Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo 

Loading required package: zoo


Attaching package: ‘zoo’


The following objects are masked from ‘package:base’:

    as.Date, as.Date.numeric

options(repr.plot.width = 15, repr.plot.height = 8)

추세를 이용한 분해법 - 가법모형

\(Z_t = T_t + S_t + I_t\), 계절주기: s
순환성분(\(C_t\))도 있지만 무시한다.

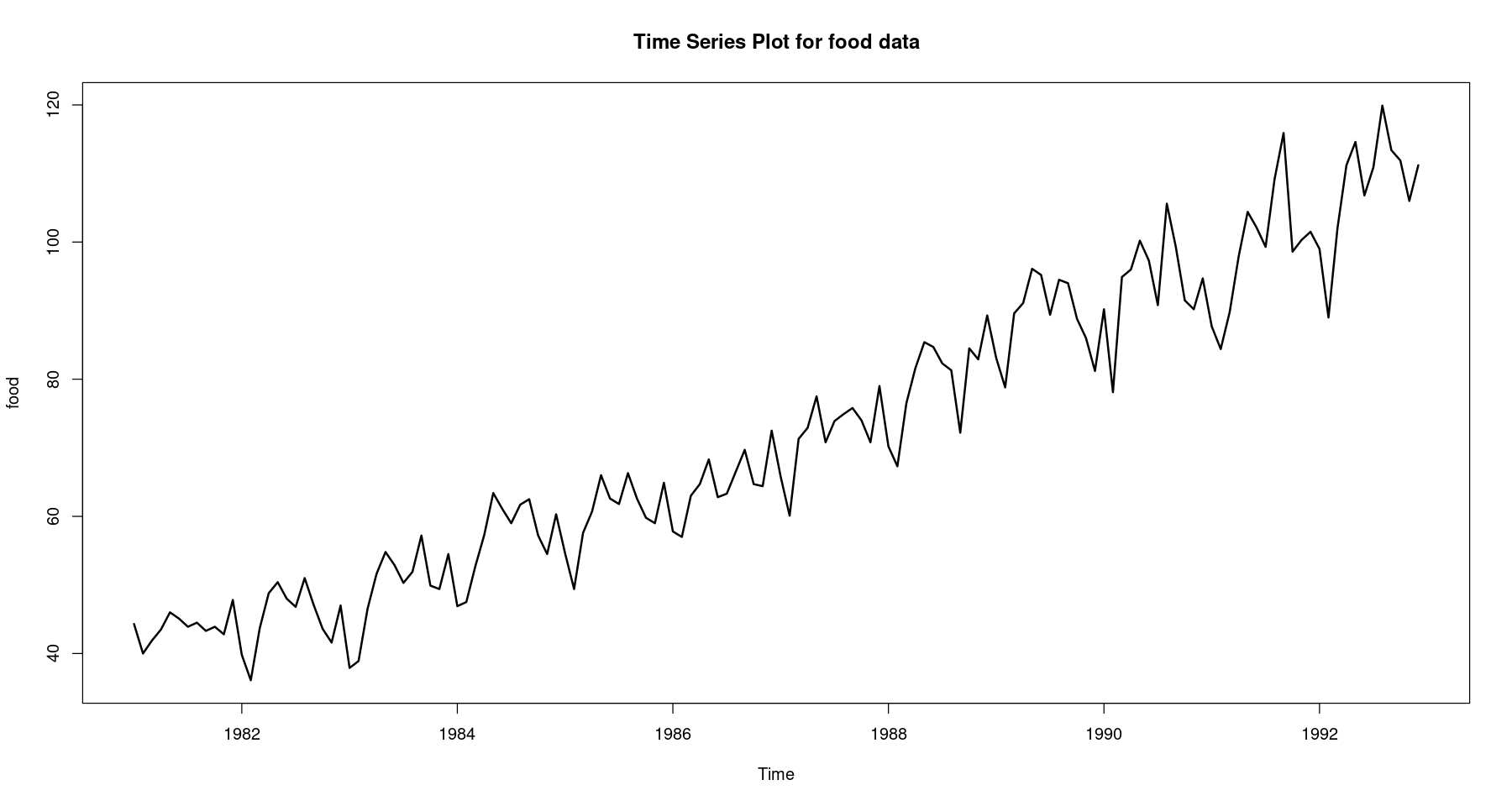
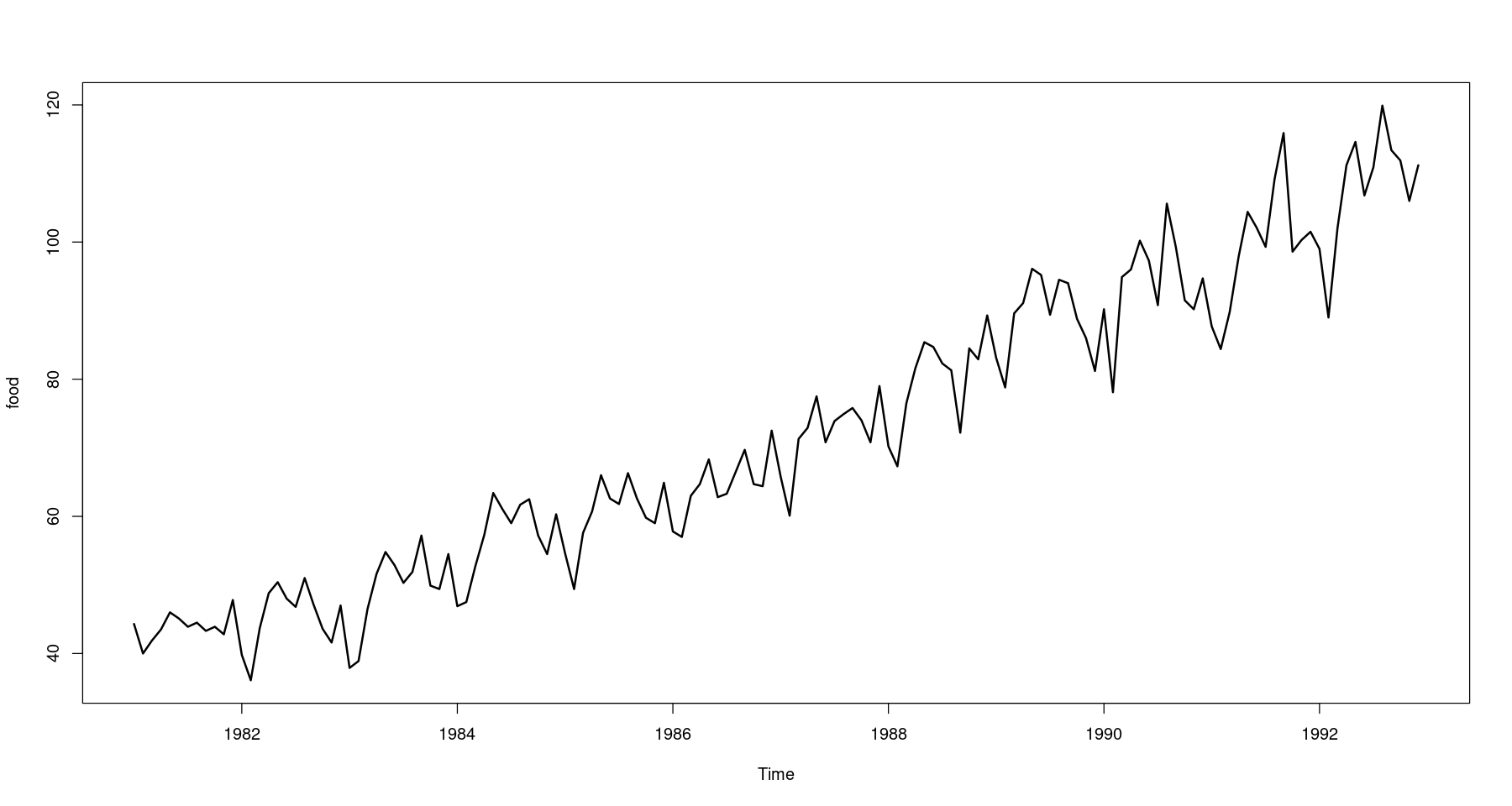
z <- scan("food.txt")
t <- 1:length(z)
food <- ts(z, start=c(1981,1), frequency=12)

plot.ts(food, lwd=2, main = "Time Series Plot for food data")

추세와 계절성분이 존재함
데이터에 이분산성이 보임, 즉 시간에 따라 계절 변동의 진폭이 증가하고 있음
가법모형을 사용하기 위해 log 변환 실행

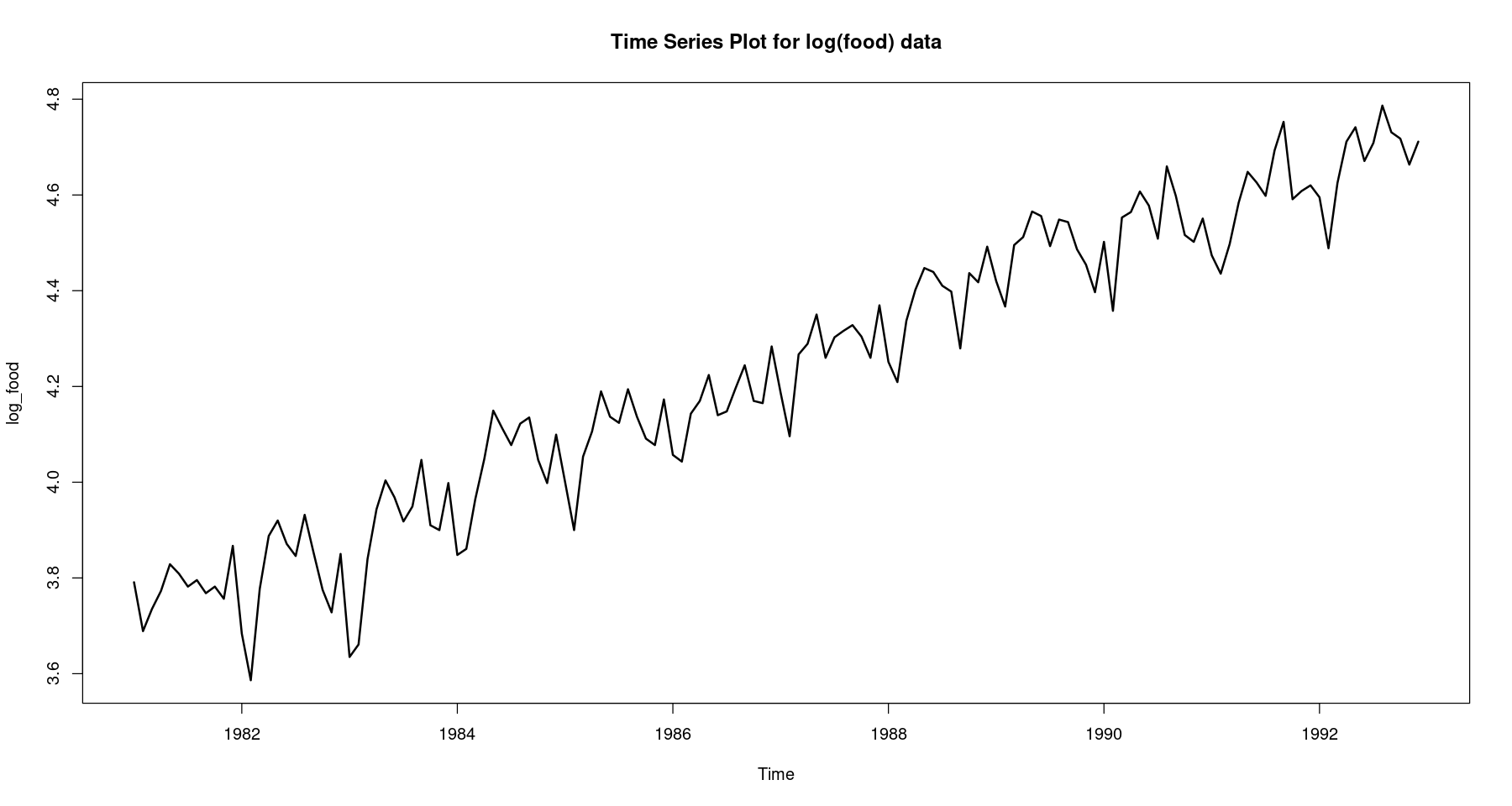
## 이분산성 제거를 위한 변수 변환
log_food <- log(food)
plot.ts(log_food, lwd=2, main = "Time Series Plot for log(food) data")

진폭이 시간의 흐름에 따라 거의 일정해 진 것을 확인할 수 있음

1. 추세성분 추정: \(Z_t = \beta_0 + \beta_1t + \epsilon_t\) 적합

fit <- lm(log_food ~ t ) 
summary(fit)


Call:
lm(formula = log_food ~ t)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.251154 -0.042190  0.009368  0.051058  0.147910 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3.705715   0.012870  287.94   <2e-16 ***
t           0.007216   0.000154   46.86   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.07682 on 142 degrees of freedom
Multiple R-squared:  0.9393,    Adjusted R-squared:  0.9388 
F-statistic:  2195 on 1 and 142 DF,  p-value: < 2.2e-16

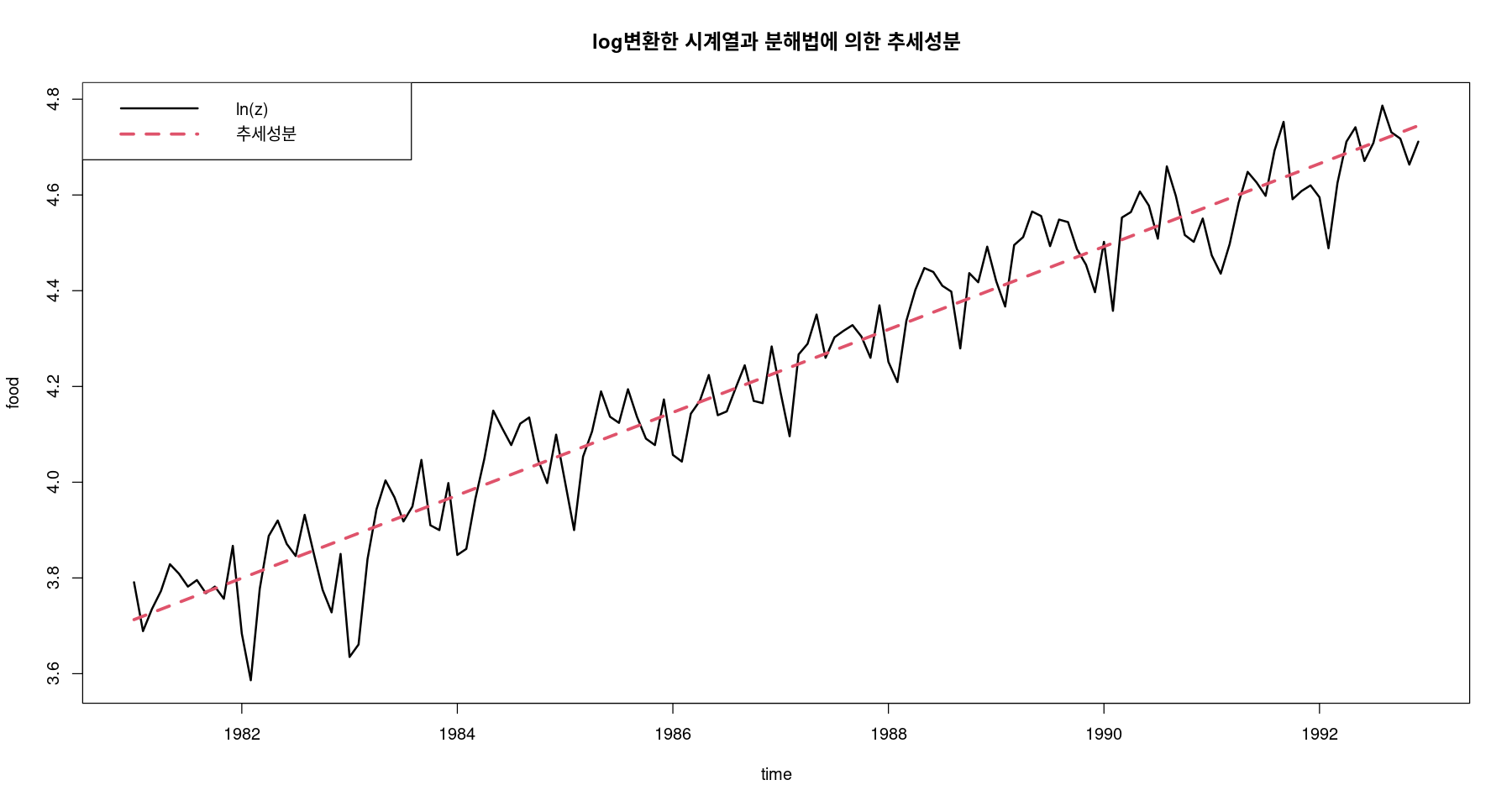
\(\hat{T}_t = 3.706 + 0.007t\)

hat_Tt <- fitted(fit)

ts.plot(log_food, hat_Tt,
     col=1:2,
     lty=1:2,
     lwd=2:3,
     ylab="food", xlab="time",
     main="log변환한 시계열과 분해법에 의한 추세성분")
legend("topleft", lty=1:2, col=1:2, lwd=2:3, c("ln(z)", "추세성분"))

2. 계절성분 추정 \(Z_t-\hat{T}_t = \delta_1I_1 + \dots + \delta_{12} I_{12} + \epsilon_t\): 적합

위에서 지시함수를 이용하여 모형 적합

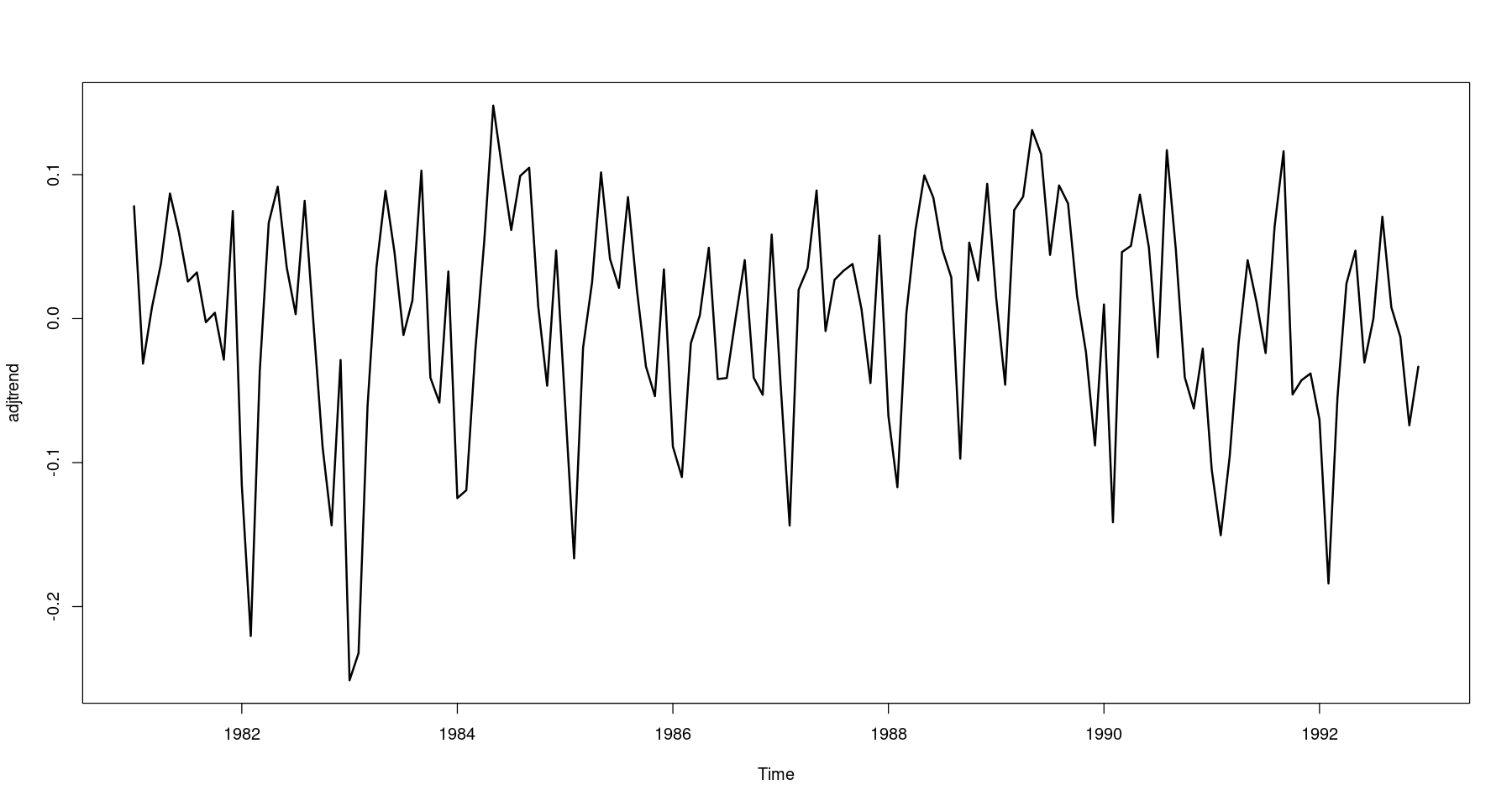
## 원시계열에서 추세성분 조정
adjtrend = log_food-hat_Tt
plot.ts(adjtrend, lwd=2)

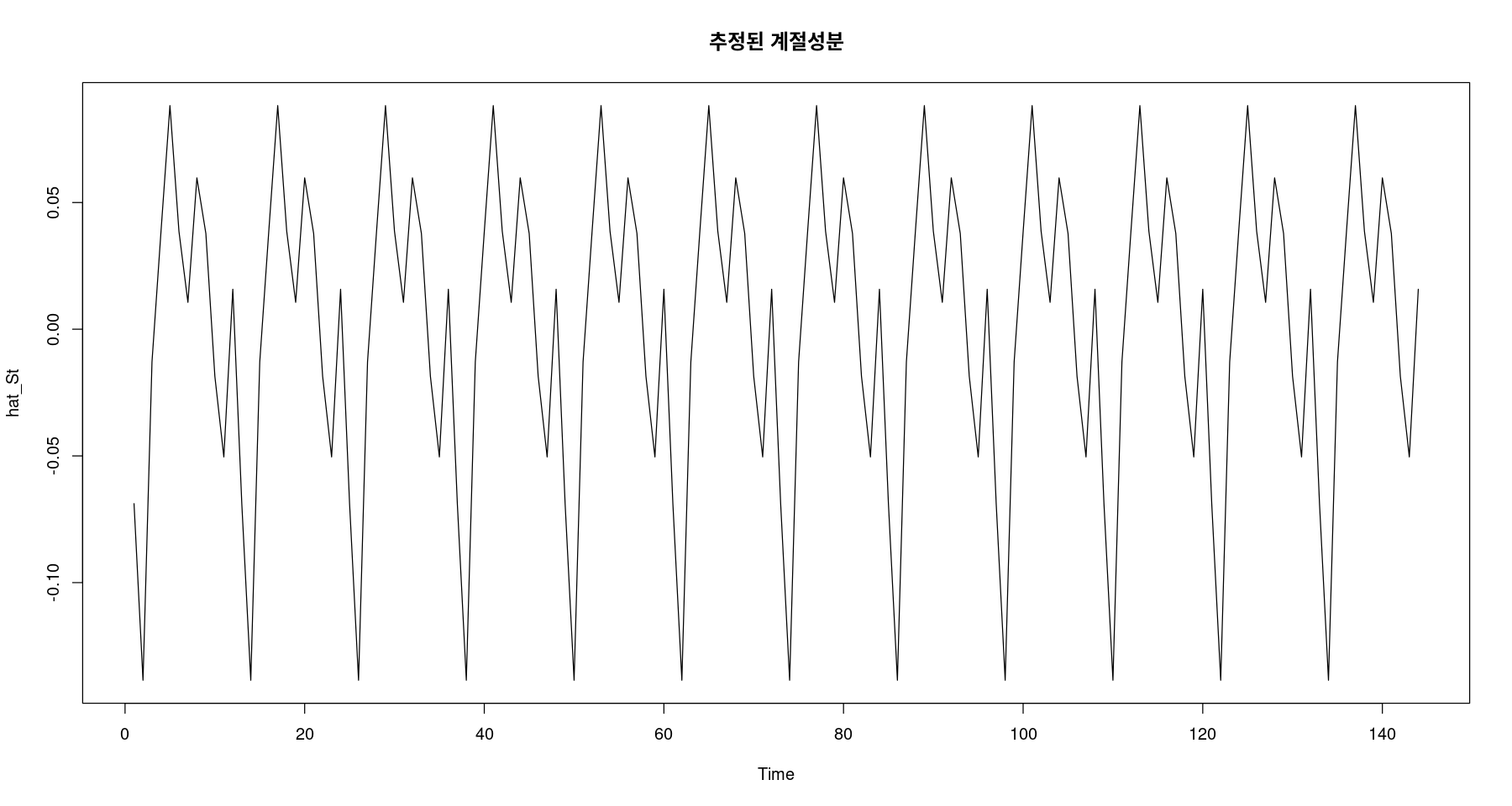
## 지시함수를 이용한 계절성분 추정
y = factor(cycle(adjtrend)) #범주형 변수로 변환

fit1 <- lm(adjtrend ~ 0+y)
summary(fit1)


Call:
lm(formula = adjtrend ~ 0 + y)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.182321 -0.028501  0.000597  0.025663  0.146887 

Coefficients:
    Estimate Std. Error t value Pr(>|t|)    
y1  -0.06883    0.01423  -4.837 3.61e-06 ***
y2  -0.13853    0.01423  -9.735  < 2e-16 ***
y3  -0.01290    0.01423  -0.907 0.366289    
y4   0.03840    0.01423   2.699 0.007872 ** 
y5   0.08825    0.01423   6.201 6.69e-09 ***
y6   0.03871    0.01423   2.720 0.007401 ** 
y7   0.01061    0.01423   0.746 0.457221    
y8   0.05972    0.01423   4.197 4.94e-05 ***
y9   0.03776    0.01423   2.653 0.008945 ** 
y10 -0.01856    0.01423  -1.304 0.194518    
y11 -0.05041    0.01423  -3.542 0.000549 ***
y12  0.01577    0.01423   1.108 0.269816    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0493 on 132 degrees of freedom
Multiple R-squared:  0.6172,    Adjusted R-squared:  0.5824 
F-statistic: 17.73 on 12 and 132 DF,  p-value: < 2.2e-16

제약조건: beta0=0이므로 각 계수들은 각 월에 평균을 의미함
\(\hat{S}_t = −0.069I_1 − 0.139I_2 + ⋯ + 0.016I_{12}\)

hat_St <- fitted(fit1)
ts.plot(hat_St, main="추정된 계절성분")

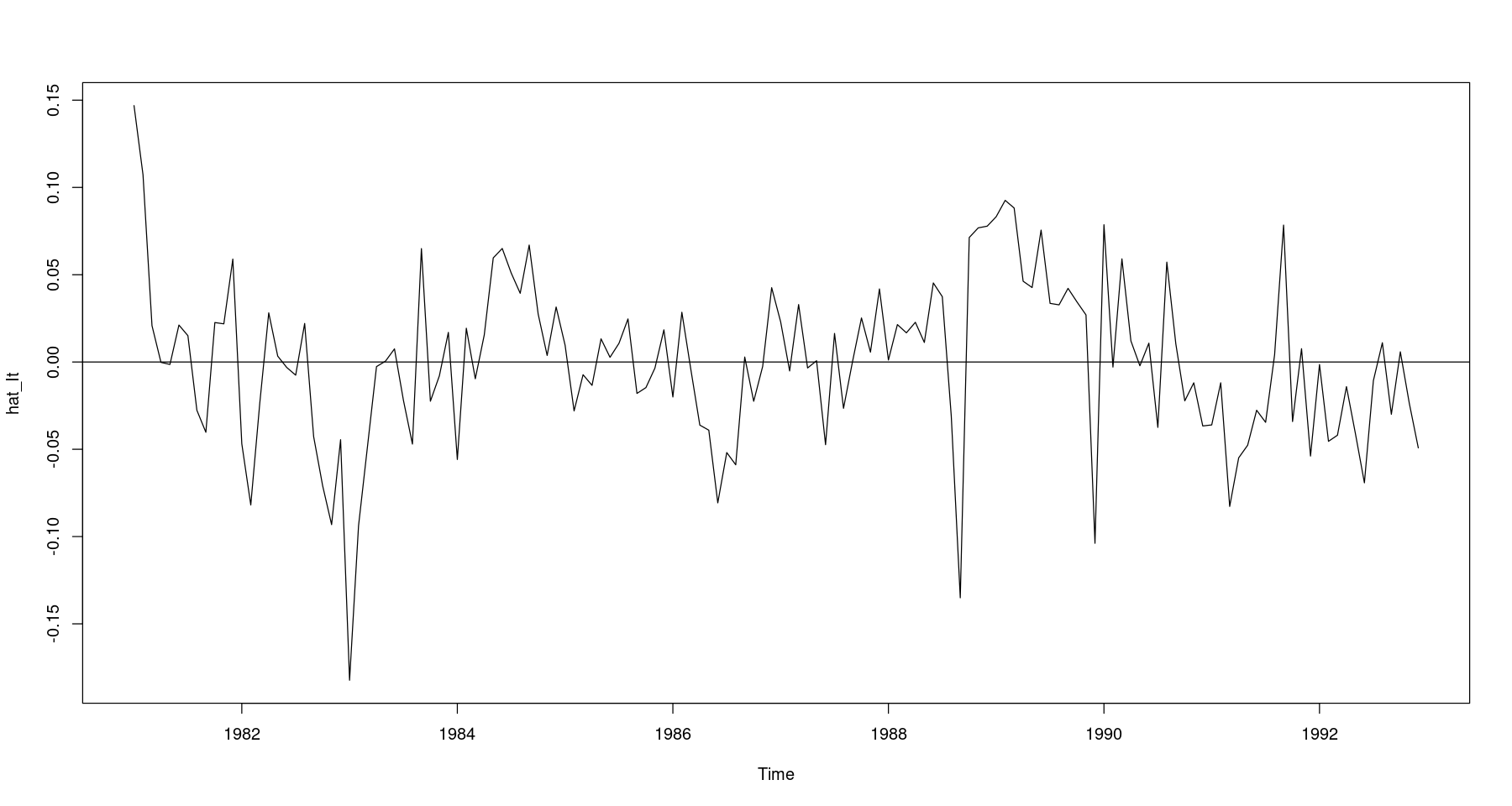
3. 불규칙 성분 \(\hat{I}_t = Z_t - \hat{T}_t - \hat{S}_t\)

hat_It <- log_food - hat_Tt - hat_St
ts.plot(hat_It); abline(h=0)

불규칙 성분들은 0을 근처로 왔다갔다 하면 좋다. 평균이 0인가?에 대한
정규분포는 크게 중요하지는 않다.

t.test(hat_It) #H0 : mu=E(It)=0


    One Sample t-test

data:  hat_It
t = 5.9991e-16, df = 143, p-value = 1
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.007801616  0.007801616
sample estimates:
   mean of x 
2.367739e-18

귀무가설을 기각할 수 없다. 즉 평균이 0이다.

hist(hat_It)

dwtest(lm(hat_It~ 1),
 alternative = 'two.sided')


    Durbin-Watson test

data:  lm(hat_It ~ 1)
DW = 1.0803, p-value = 2.748e-08
alternative hypothesis: true autocorrelation is not 0

오차가 uncorrelected인지 확인해야함..
양의 상관관계가 있어보인다.

bptest이용해서 등분산성/이분사넛ㅇ 확인해야함.. -> 자꾸 오류나넹

4. 추정 \(\hat{Z}_t = \hat{T}_t + \hat{S}_t\)

체계적 성분: 추세, 계절 성분
비체계적 성분: 불규칙 성분

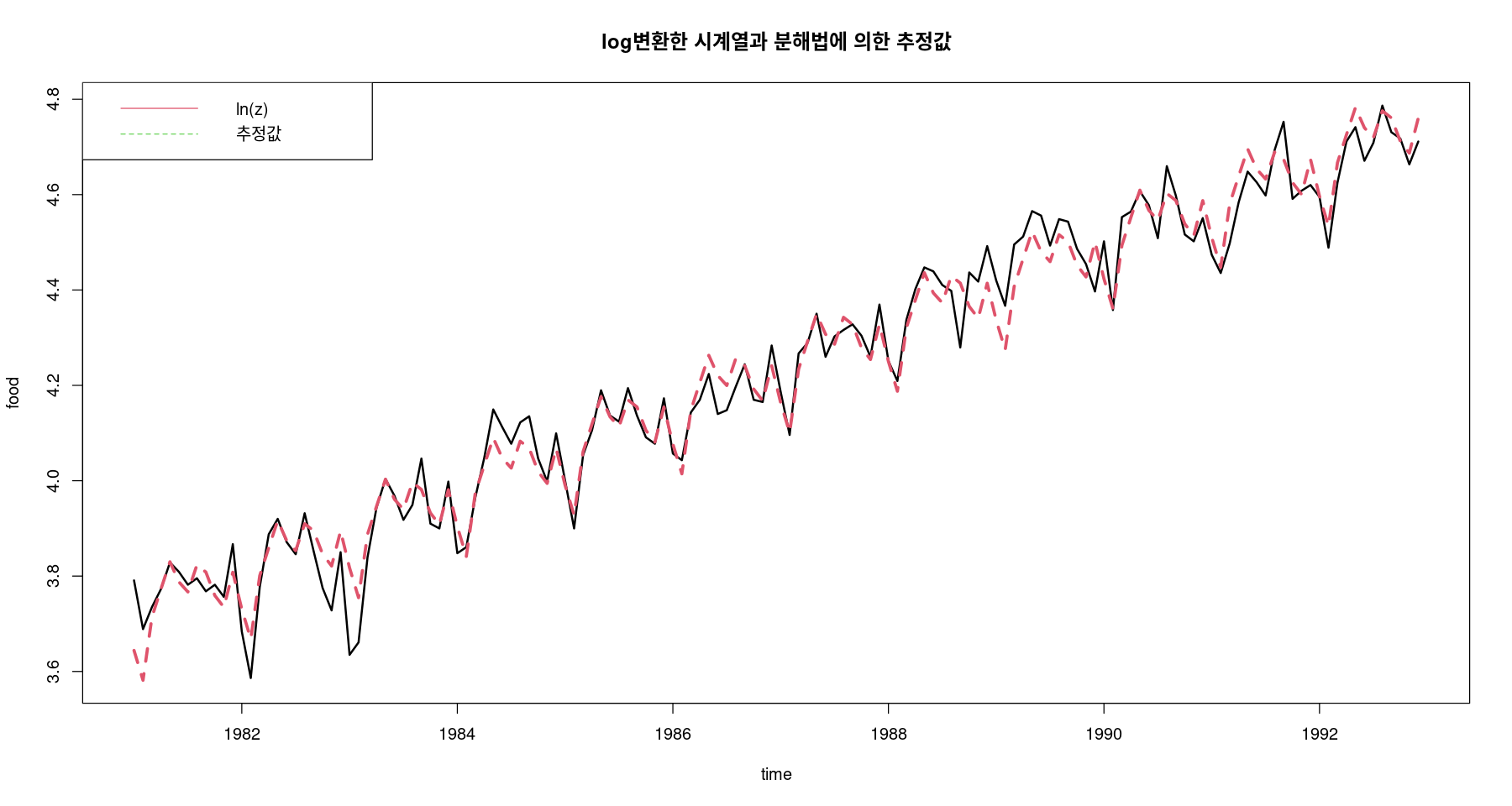
pred_a <- hat_Tt + hat_St

ts.plot(log_food, pred_a, col=1:2, lty=1:2, lwd=2:3,ylab="food", xlab="time",
     main="log변환한 시계열과 분해법에 의한 추정값")
legend("topleft", lty=1:2, col=2:3, c("ln(z)", "추정값"))

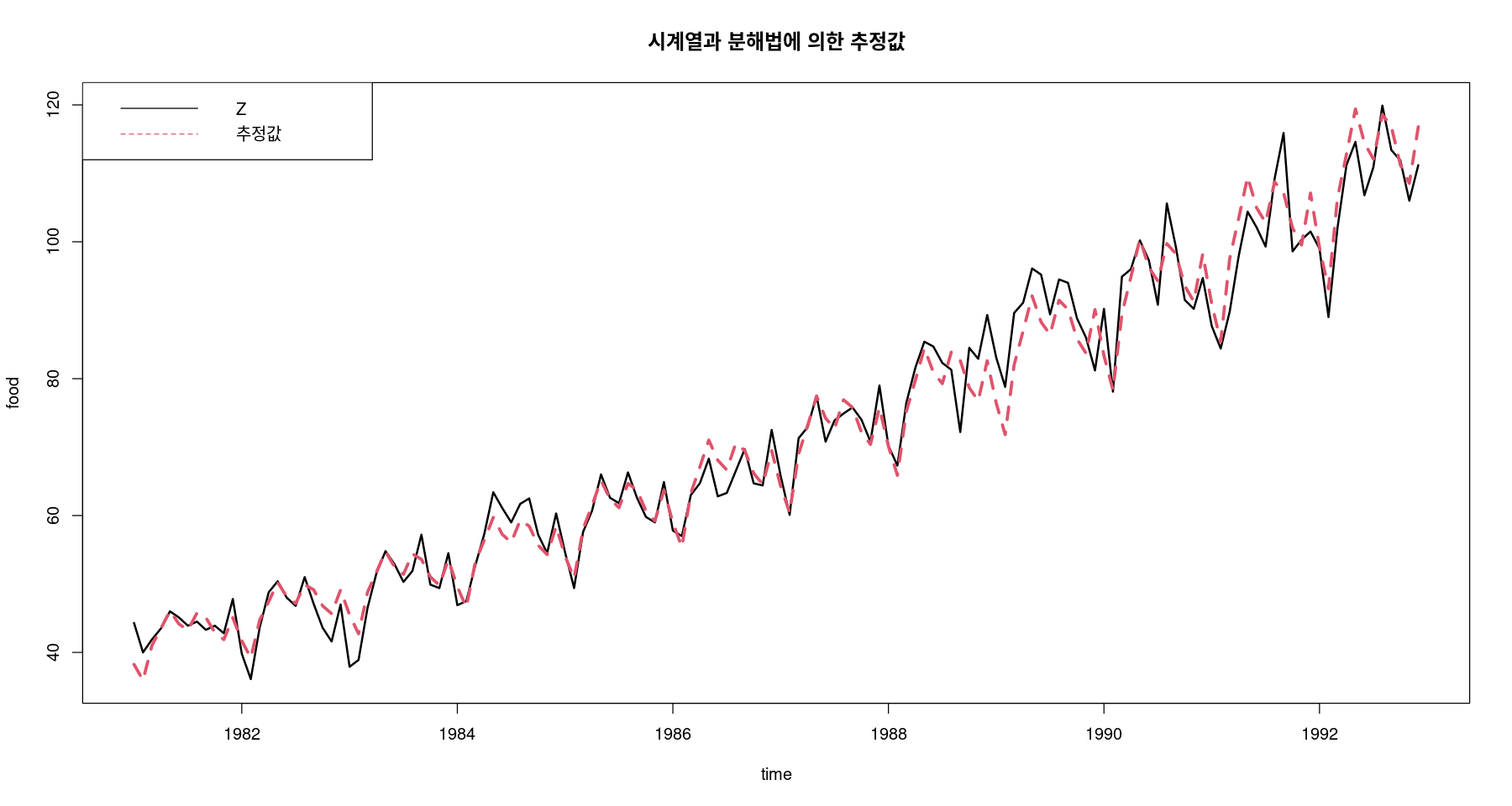
ts.plot(food, exp(pred_a), col=1:2, lty=1:2, lwd=2:3,ylab="food", xlab="time",
     main="시계열과 분해법에 의한 추정값")
legend("topleft", lty=1:2, col=1:2, c("Z", "추정값"))

SSE/MSE 구할 때 로그 변환 했던 데이터 -> 오리지널 데이터로 변환해서 비교해야함!!!

SSE = sum((food-exp(pred_a))^2)
MSE = mean((food-exp(pred_a))^2)
SSE
MSE

1636.87967934919

11.3672199954805

추세를 이용한 분해법 - 승법모형

\(Z_t = T_t \times S_t \times I_t\), 계절주기:s

plot.ts(food, lwd=2)

1. 추세성분 추정: \(Z_t = \beta_0 + \beta_1t + \epsilon_t\) 적합

## 추세성분 추정
fit3 <- lm(food ~ t ) 
summary(fit3)


Call:
lm(formula = food ~ t)

Residuals:
     Min       1Q   Median       3Q      Max 
-14.0331  -3.4505  -0.1355   4.2911  15.3948 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 35.28614    0.95561   36.92   <2e-16 ***
t            0.50557    0.01143   44.21   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.704 on 142 degrees of freedom
Multiple R-squared:  0.9323,    Adjusted R-squared:  0.9318 
F-statistic:  1955 on 1 and 142 DF,  p-value: < 2.2e-16

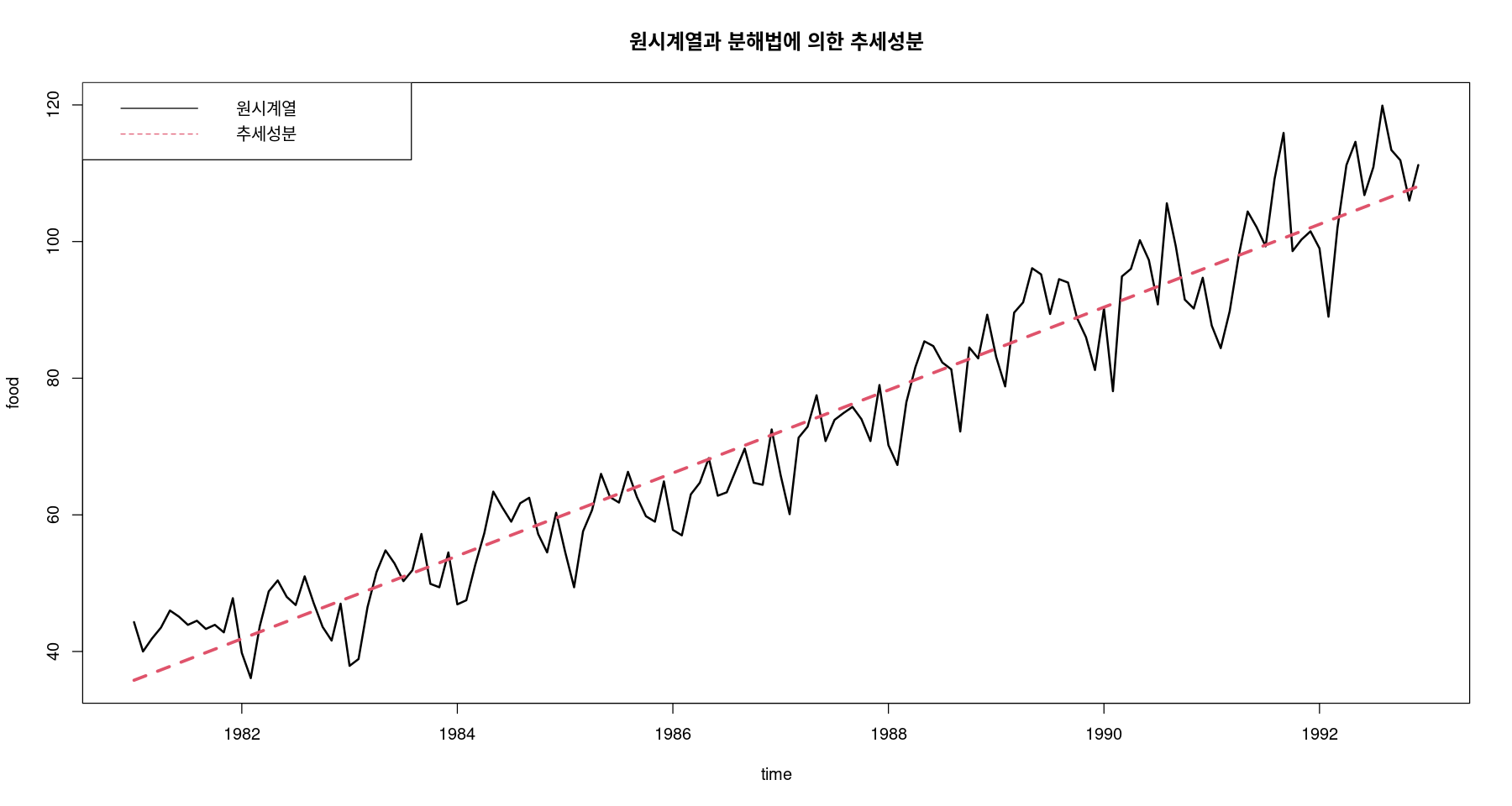
\(\hat{T}_t = 35.286 + 0.506t\)

ts.plot(food, fitted(fit3) , col=1:2, lty=1:2, lwd=2:3, ylab="food", xlab="time",
 main="원시계열과 분해법에 의한 추세성분")
legend("topleft", lty=1:2, col=1:2, c("원시계열", "추세성분"))

약간 2차가 있어보인다.

fit4 <- lm(food ~ t+I(t^2)) 
summary(fit4)


Call:
lm(formula = food ~ t + I(t^2))

Residuals:
    Min      1Q  Median      3Q     Max 
-16.845  -3.535   0.566   3.523  13.391 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 4.011e+01  1.346e+00  29.799  < 2e-16 ***
t           3.071e-01  4.286e-02   7.166 3.96e-11 ***
I(t^2)      1.369e-03  2.863e-04   4.779 4.37e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.31 on 141 degrees of freedom
Multiple R-squared:  0.9417,    Adjusted R-squared:  0.9409 
F-statistic:  1139 on 2 and 141 DF,  p-value: < 2.2e-16

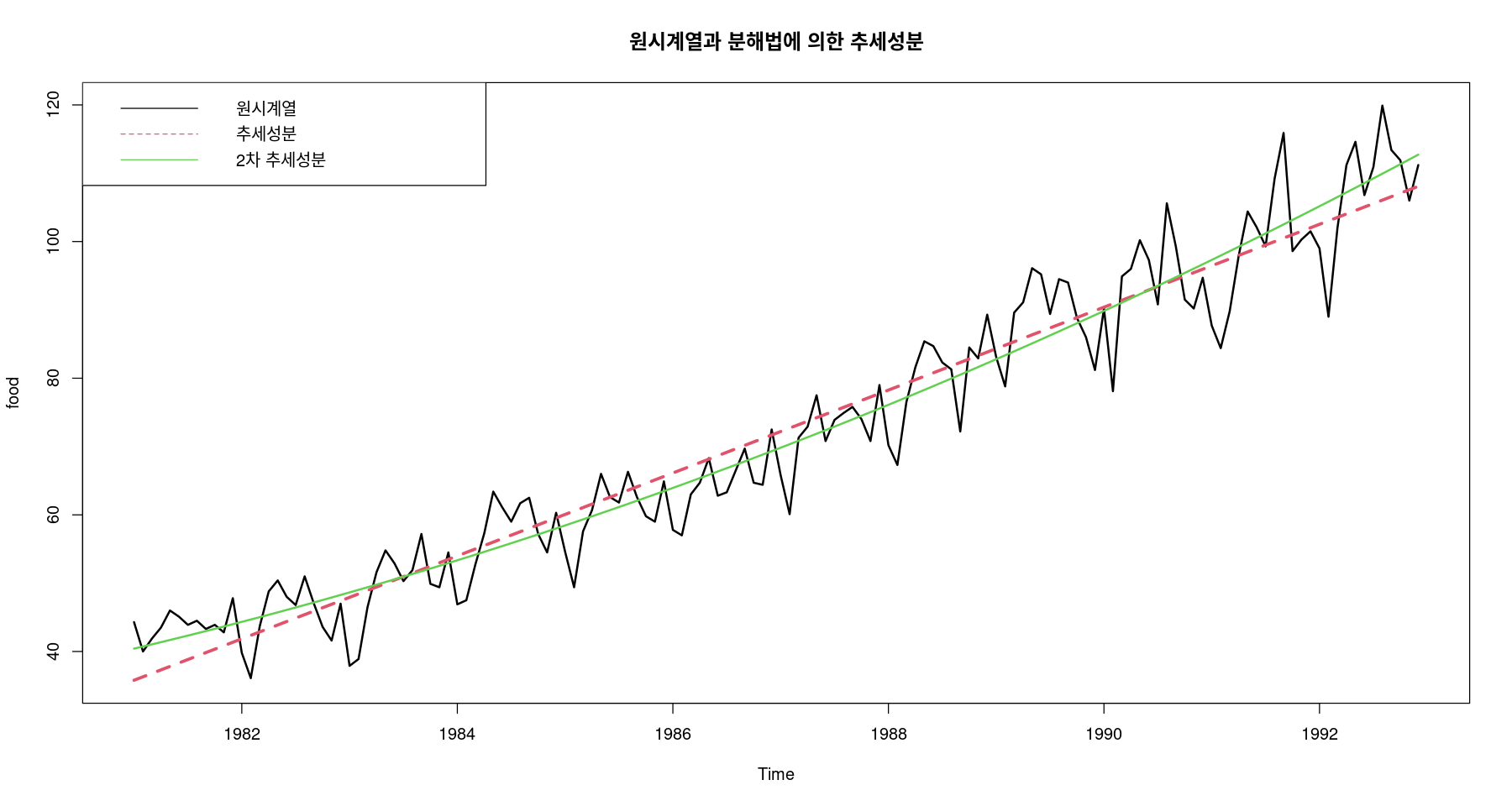
ts.plot(food, fitted(fit3), fitted(fit4), col=1:3, lty=1:2, lwd=2:3, ylab="food",
 main="원시계열과 분해법에 의한 추세성분")
legend("topleft", lty=1:2, col=1:3, c("원시계열", "추세성분", "2차 추세성분"))

2. 계절성분 추정 \(Z_t / \hat{T}_t = \delta_1I_1 + \dots + \delta_{12} I_{12} + \epsilon_t\): 적합

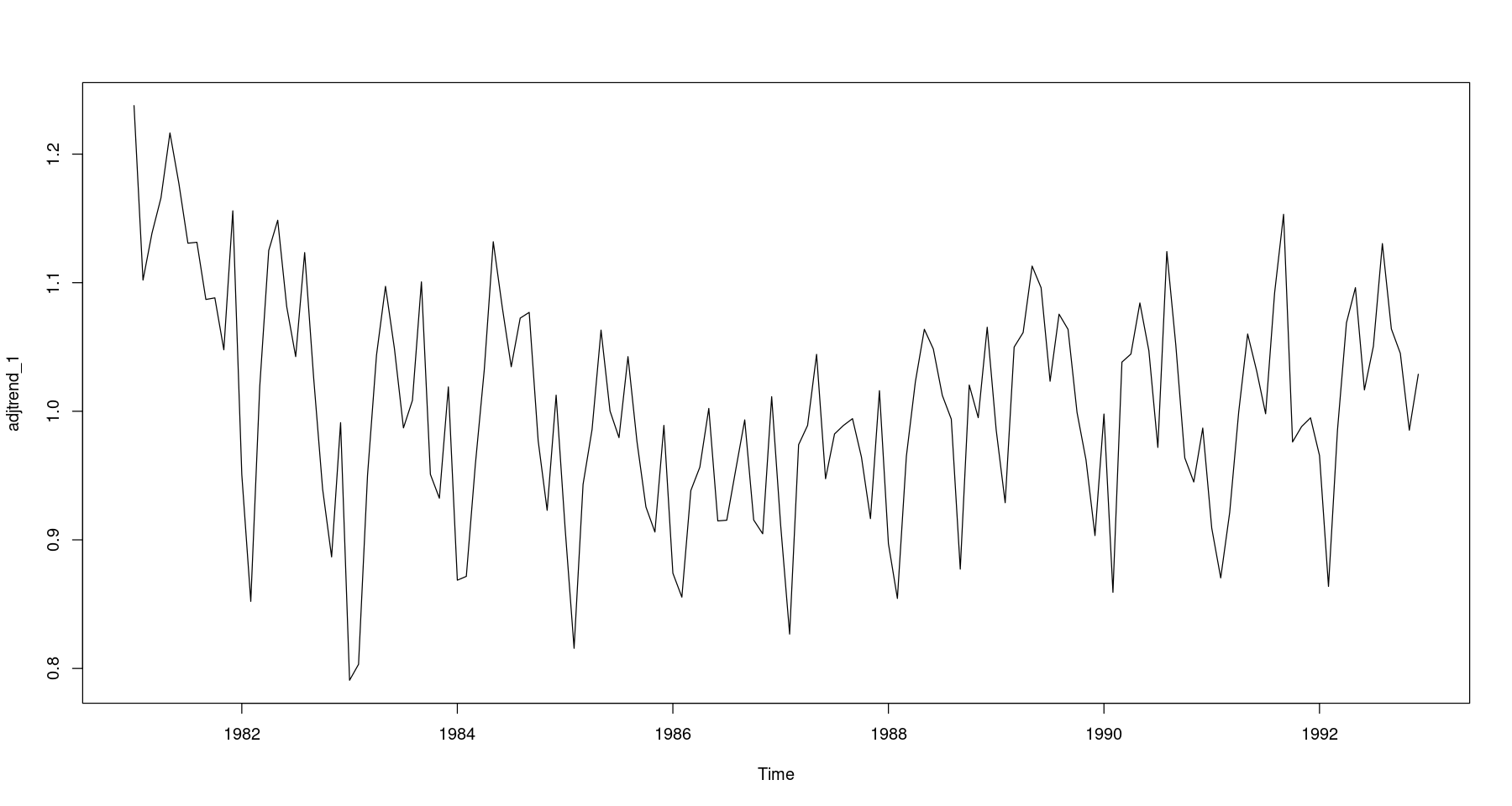
## 원시계열에서 추세성분 조정
trend_1 = fitted(fit3)  # fit3:1차 추세모형
adjtrend_1 = food/trend_1
plot.ts(adjtrend_1)

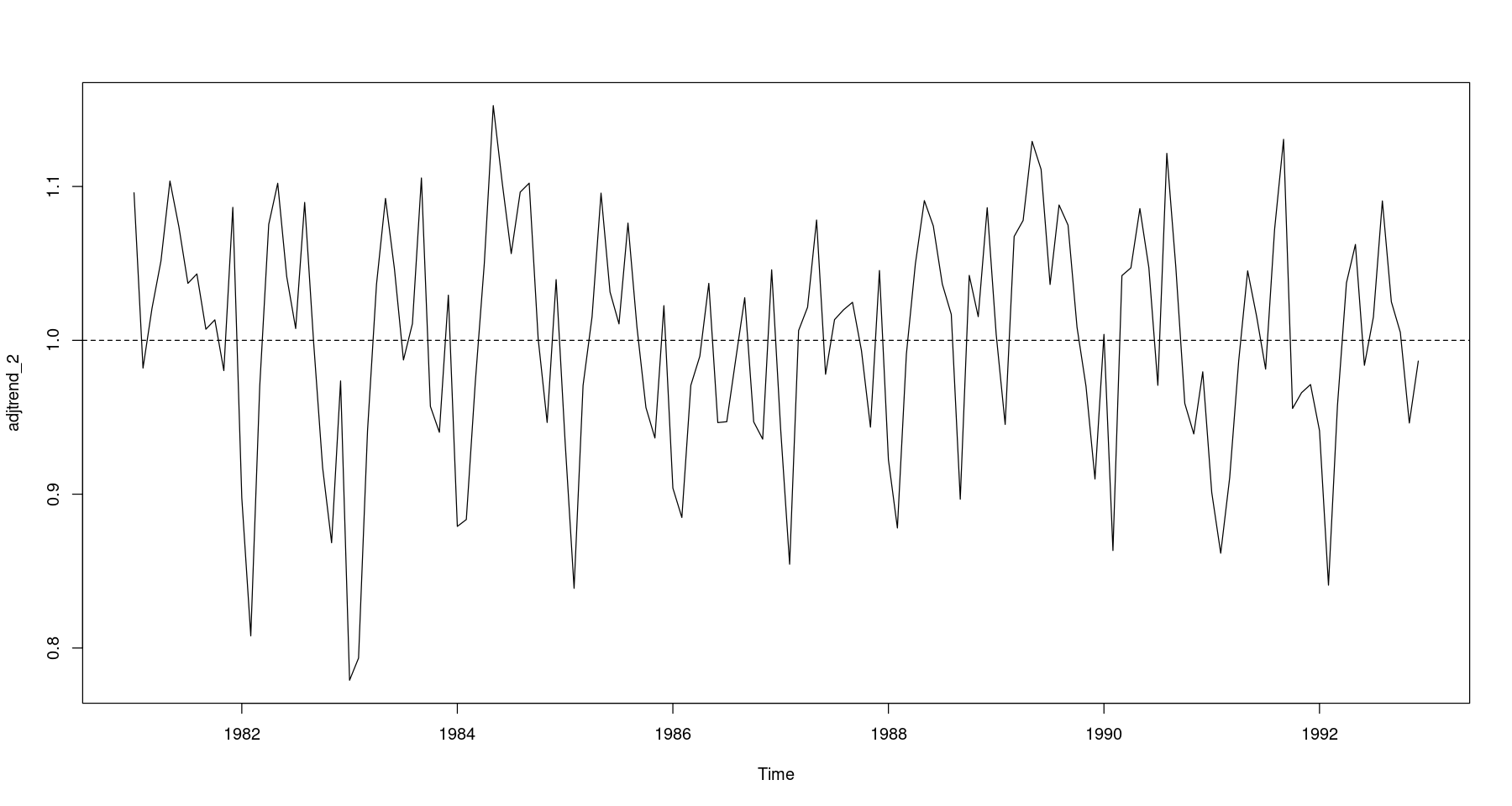
## 원시계열에서 2차 추세성분 조정
trend_2 = fitted(fit4)  # fit4: 2차 추세모형
adjtrend_2 = food/trend_2
plot.ts(adjtrend_2)
abline(h=1, lty=2)

## 지시함수를 이용한 계절성분 추정
y = factor(cycle(adjtrend_2)) 
fit5 <- lm(adjtrend_2 ~ 0+y)
summary(fit5)


Call:
lm(formula = adjtrend_2 ~ 0 + y)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.154659 -0.027736  0.000622  0.028345  0.162186 

Coefficients:
    Estimate Std. Error t value Pr(>|t|)    
y1   0.93372    0.01368   68.23   <2e-16 ***
y2   0.86951    0.01368   63.54   <2e-16 ***
y3   0.98517    0.01368   72.00   <2e-16 ***
y4   1.03650    0.01368   75.75   <2e-16 ***
y5   1.08954    0.01368   79.62   <2e-16 ***
y6   1.03763    0.01368   75.83   <2e-16 ***
y7   1.00829    0.01368   73.69   <2e-16 ***
y8   1.05940    0.01368   77.42   <2e-16 ***
y9   1.03744    0.01368   75.82   <2e-16 ***
y10  0.97966    0.01368   71.59   <2e-16 ***
y11  0.94903    0.01368   69.35   <2e-16 ***
y12  1.01466    0.01368   74.15   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0474 on 132 degrees of freedom
Multiple R-squared:  0.998, Adjusted R-squared:  0.9978 
F-statistic:  5359 on 12 and 132 DF,  p-value: < 2.2e-16

\(\hat{S}_t = 0.934I_1 + 0.870I_2 + ⋯ + 1.015I_{12}\)

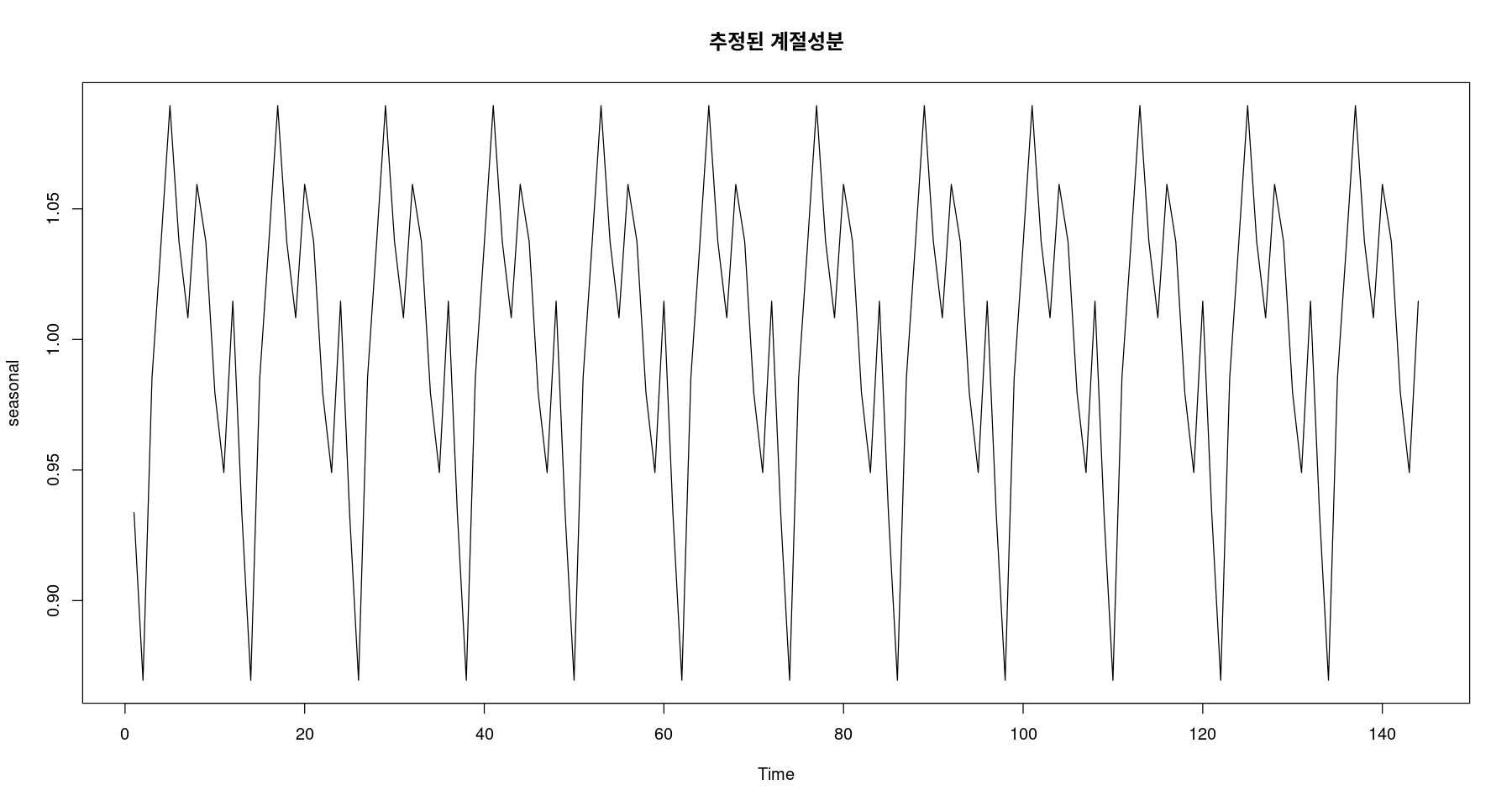
seasonal <- fitted(fit5)
ts.plot(seasonal, main="추정된 계절성분")

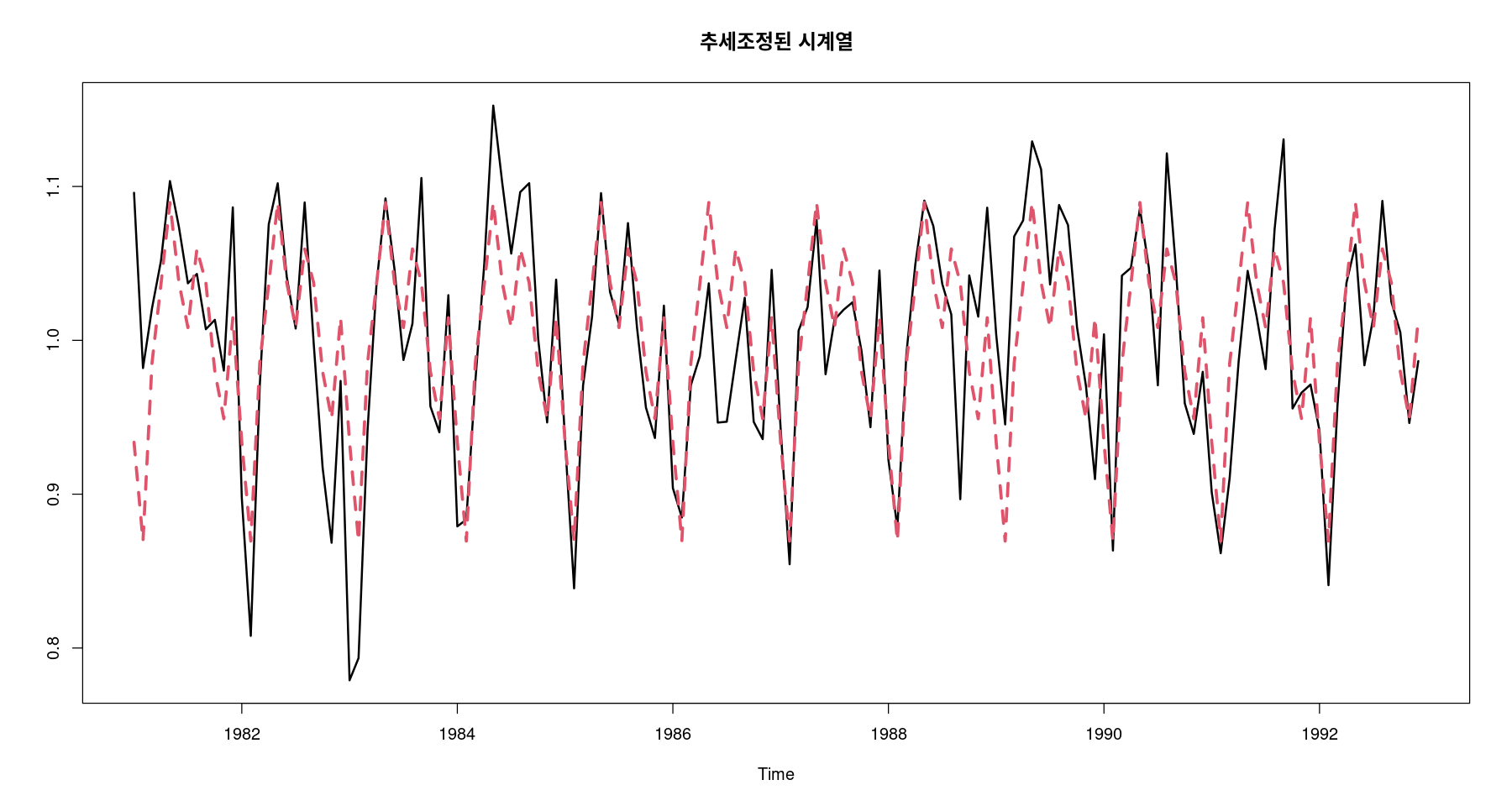
seasonal <- fitted(fit5)
ts.plot(adjtrend_2, seasonal, col=1:2, lty=1:2, lwd=2:3, main="추세조정된 시계열")

3. 불규칙 성분 \(\hat{I}_t = Z_t / ( \hat{T}_t \times \hat{S}_t)\)

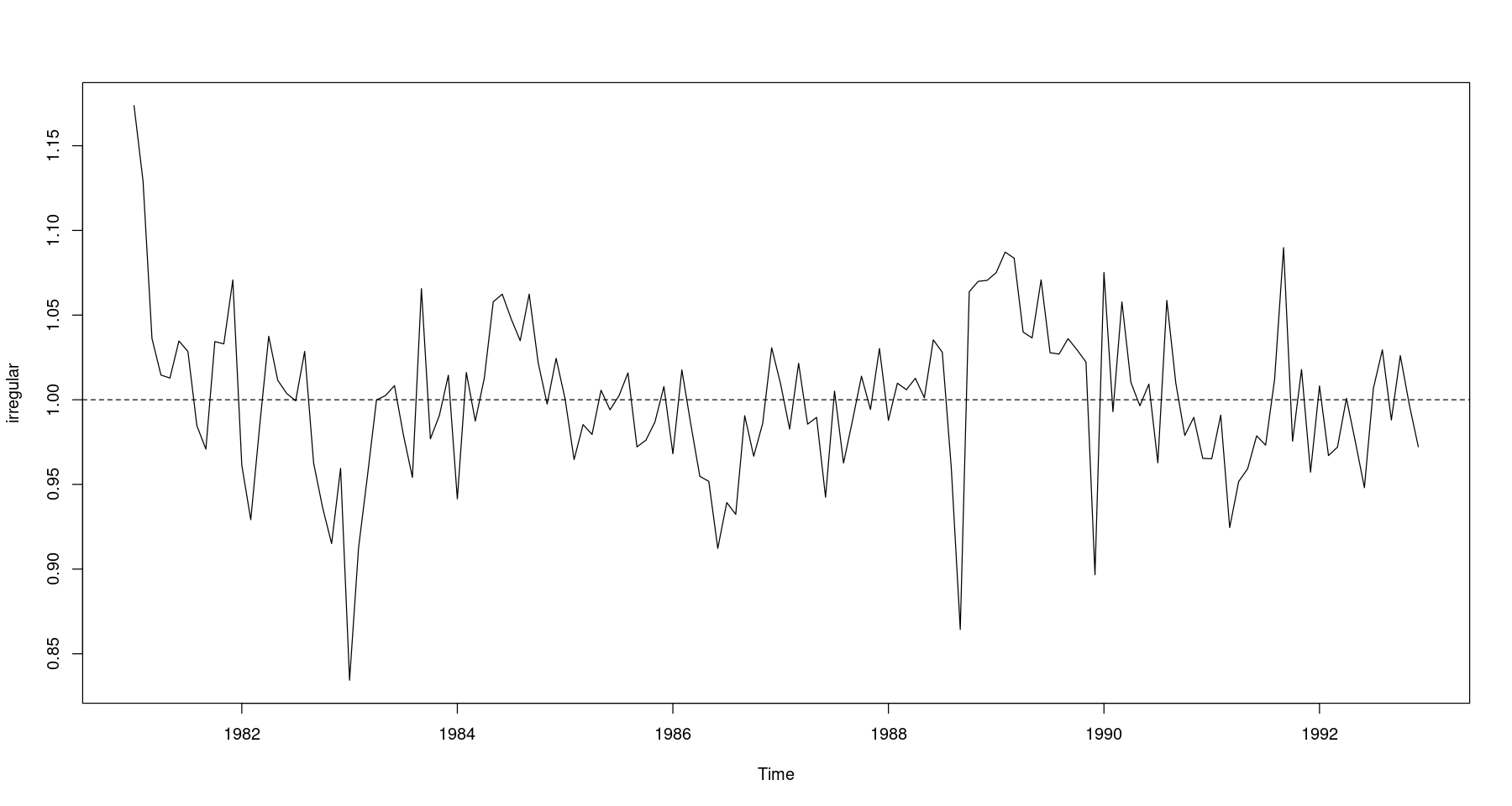
irregular <- food/trend_2/seasonal

ts.plot(irregular); abline(h=1, lty=2)

t.test(irregular, mu=1)


    One Sample t-test

data:  irregular
t = 0, df = 143, p-value = 1
alternative hypothesis: true mean is not equal to 1
95 percent confidence interval:
 0.9923514 1.0076486
sample estimates:
mean of x 
        1

나눠준거기 떄문에.. 비슷하면 1이랑 가까워지니까 mu=1과 비교하는 것

dwtest(lm(irregular~ 1), alternative = 'two.sided')


    Durbin-Watson test

data:  lm(irregular ~ 1)
DW = 1.0897, p-value = 3.799e-08
alternative hypothesis: true autocorrelation is not 0

4. 추정 \(\hat{Z}_t = \hat{T}_t \times \hat{S}_t\)

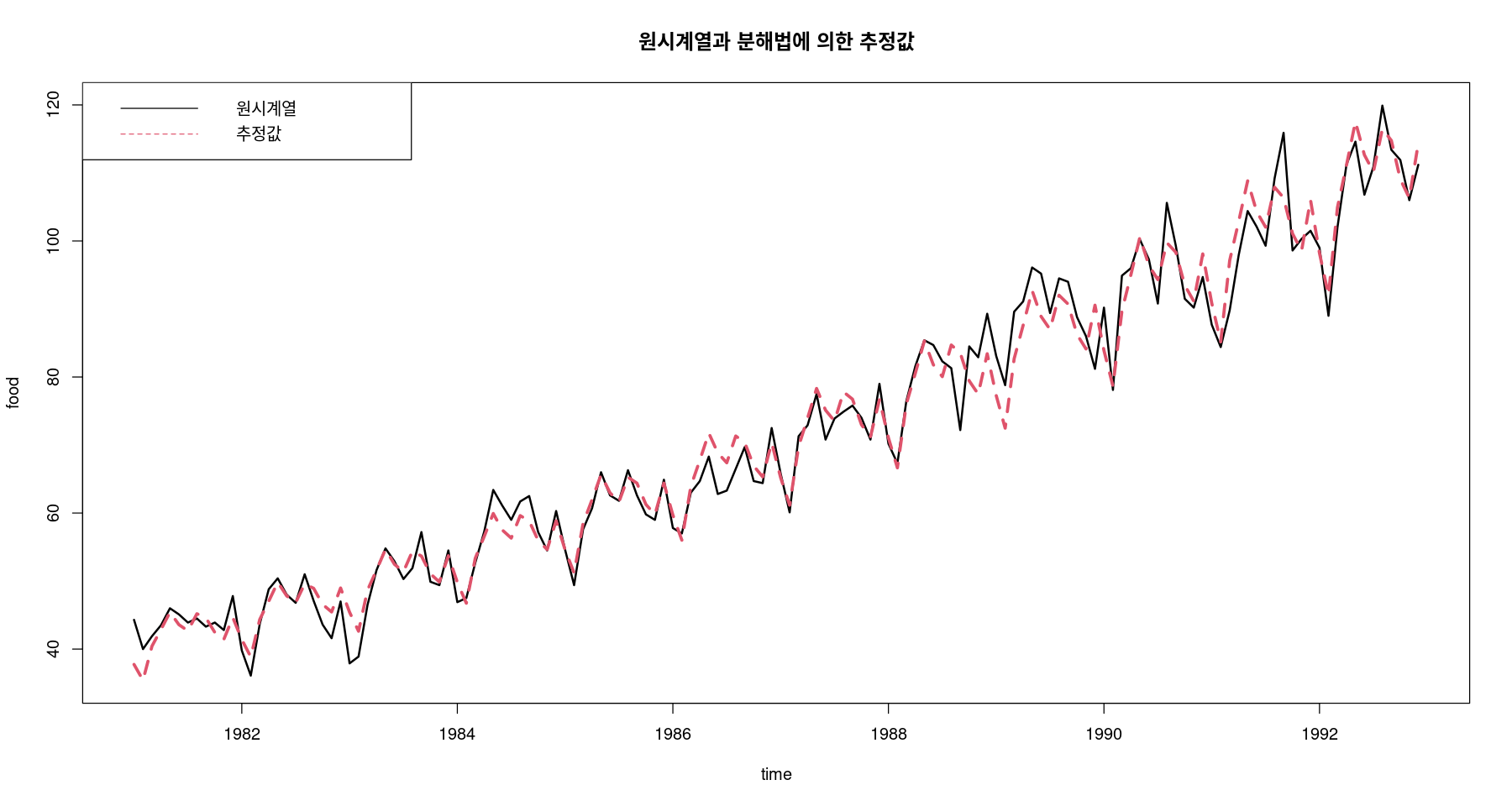
pred_m <- trend_2 * seasonal

ts.plot(food, pred_m, col=1:2, lty=1:2, lwd=2:3, ylab="food", xlab="time",
 main="원시계열과 분해법에 의한 추정값")
legend("topleft", lty=1:2, col=1:2, c("원시계열", "추정값"))

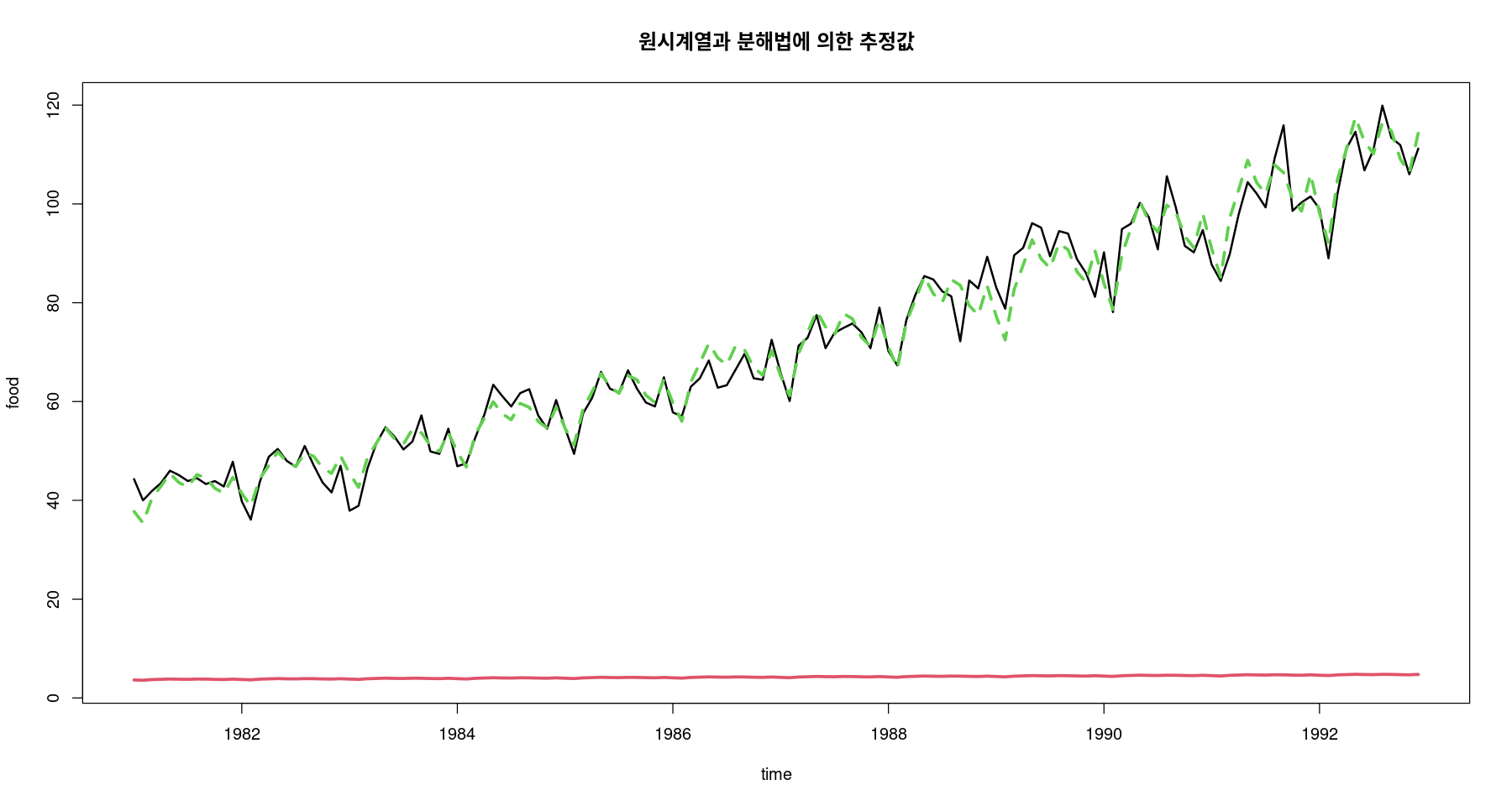
#pred_a #가법
#pred_m #승법
ts.plot(food, pred_a, pred_m, col=1:3, lty=c(1,1,2), lwd=c(2,3,3), ylab="food", xlab="time",
     main="원시계열과 분해법에 의한 추정값")

pred_a는 원 food데이터에서 log를 취한 값이라 그런지,, 빨간색 선..

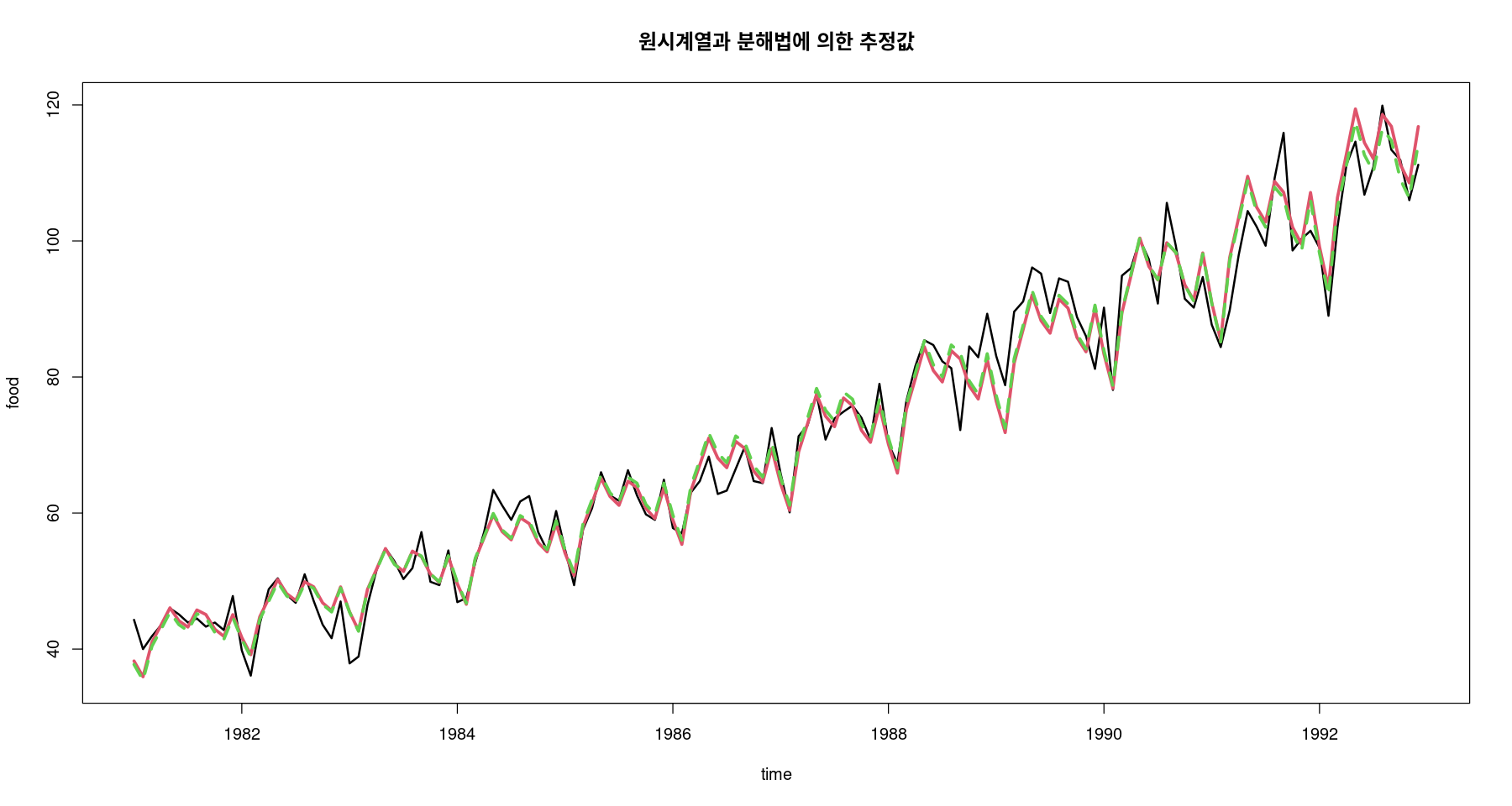
#pred_a #가법
#pred_m #승법
ts.plot(food, exp(pred_a), pred_m, col=1:3, lty=c(1,1,2), lwd=c(2,3,3), ylab="food", xlab="time",
     main="원시계열과 분해법에 의한 추정값")

pred_a에 다시 exp를 취해줬다.

SSE/MSE비교

#가법
sum((food-exp(pred_a))^2) ##SSE
mean((food-exp(pred_a))^2) ##MSE

1636.87967934919

11.3672199954805

#승법
sum((food-pred_m)^2) #SSE
mean((food-pred_m)^2) #MSE

1483.03817025796

10.298876182347